很久之前就像好好学习一下姿态解算的算法,最近下定决心把这些看了一下。
在刚开始,我们定义两个坐标系:世界坐标系(也叫惯性坐标系)、飞行器坐标系。世界坐标系静止不动,而飞行器坐标系则与是固连在飞行器上的。
欧拉角:俯仰角、横滚角、偏航角,分别表示绕y x z 轴旋转的角度。
需要注意的是,欧拉角表示的是相对于飞行器坐标系的角度。因此,欧拉角与旋转的顺序是相关的
表达旋转的方式有多种,如方向余弦、四元数、欧拉角等
其中,方向余弦计算量较大,欧拉角有“万向死锁”问题(当欧拉角达到90°的时候会出现),因此很多飞控都使用四元数进行姿态解算。
四元数的定义:(单位四元数,类似于单位复数能表示二位平面内的旋转一样)
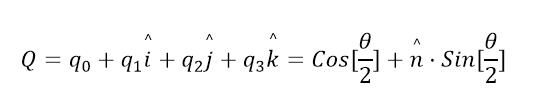
其中 n 为转轴方向, Θ� 2 ⁄ 为转角大小, i, j, k的关系为:
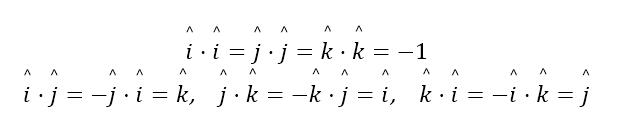
其实挺容易理解,i,j,k既有虚数的性质,又有向量的性质。
虚数的性质体现在:i i=-1 ,向量的性质则体现在,两个向量的(外)积等于与这两个向量垂直的第三个向量,即ij=k
需要注意的是,四元数不满足乘法交换律
若有一个四元数来表示按照ZYX三轴顺序进行旋转,则这个四元数可以表示为:(四元数的相乘,表示为旋转的组合)
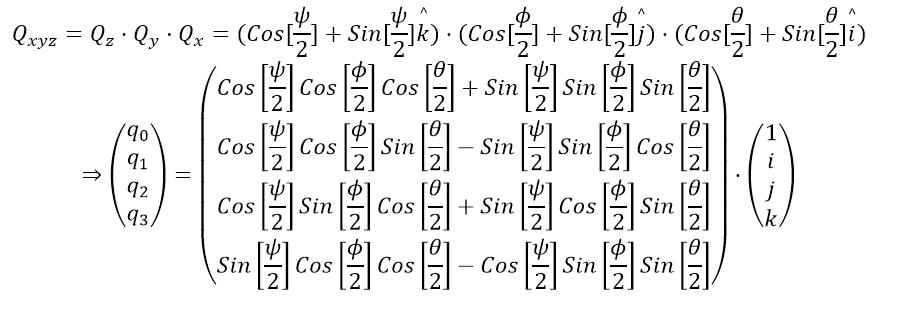


由此,我们得到了一个四元数的旋转矩阵Mq与欧拉角的关系,也就是说只要我们能得到飞行器在任意时刻的四元数表示(q0,q1,q2,q3),那么我们就能计算出Mq,从而得到三个欧拉角。
那么问题来了,我们如何得到任意时刻的四元数表示呢?需要进行四元数的更新。
由一阶龙哥库塔可得:
Q(t+△t)=Q(t)+△t*dQ(t)/dt
可以看出,需要计算Q(t)的微分才能更新四元数

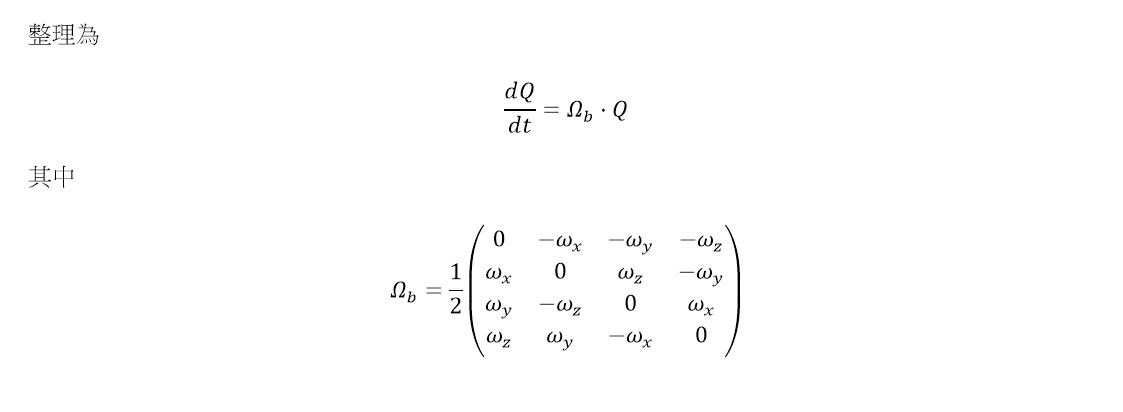
代入龙哥库塔:
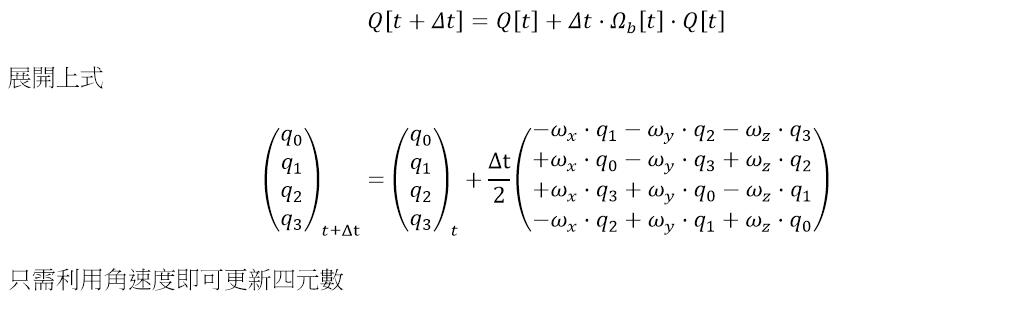
通过这里,我们就能得到任意时刻的四元数表示了,此时我们还只用到了陀螺仪。
显然,陀螺仪由于积分误差,无法长时间正常工作,我们需要引入加速度计对其进行矫正。

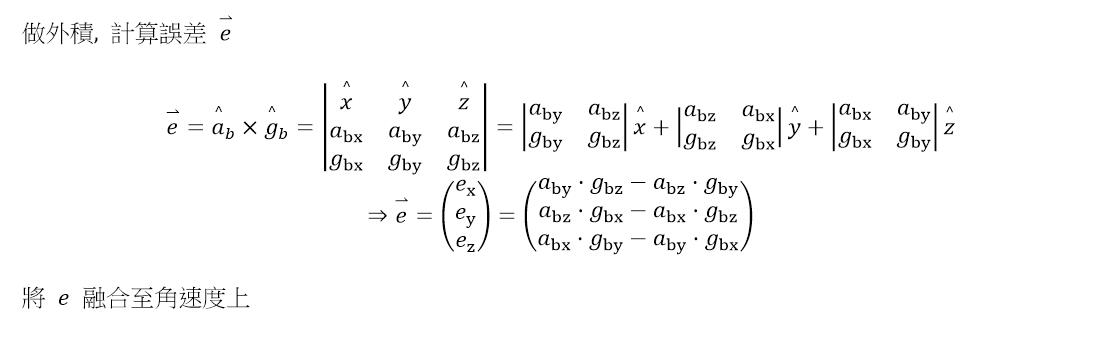
为什么需要对加速度计进行归一化呢?
因为做外积的时候,当两个向量的模都为1,那么外积的结果就是sin<a,b>,当<a,b>较小的时候,我们就认为sin<a,b>就是<a,b>,那么向量a、b间的夹角,不就是我们需要的一个误差表示吗?
至此,姿态解算推导就差不多完毕了。
以上就是IMU_Update算法的所有内容。实际上,这个算法的Yaw时间久了之后也会漂移,因为加速度计并不能对yaw进行校准。因此,若想进一步获得准确的偏航角,则需要引入磁力计了。